LINEAR EQUATIONS - GAUSSIAN ELIMINATION
----------------------------------------------------------

WANT FREE COACHING IN MATHS IN BANGALORE ?
CALL 9480193388 OR EMAIL freemaths10212@gmail.com

For details see post on 26-Feb-2015 at 6:00 am.

----------------------------------

Attempt to solve the following linear systems by using Gaussian elimination to find a similar system whose coefficient matrix is in row echelon form.

If the system has a unique solution, give it (in point form.)

If the system is inconsistent, write NONE for the solutions.

If the system is consistent and there are free variables, transform it to reduced row echelon form and find all solutions. (Write your general solutions in terms of the variables a, b, c, .... For example, (1,2-a+b,b,a).)

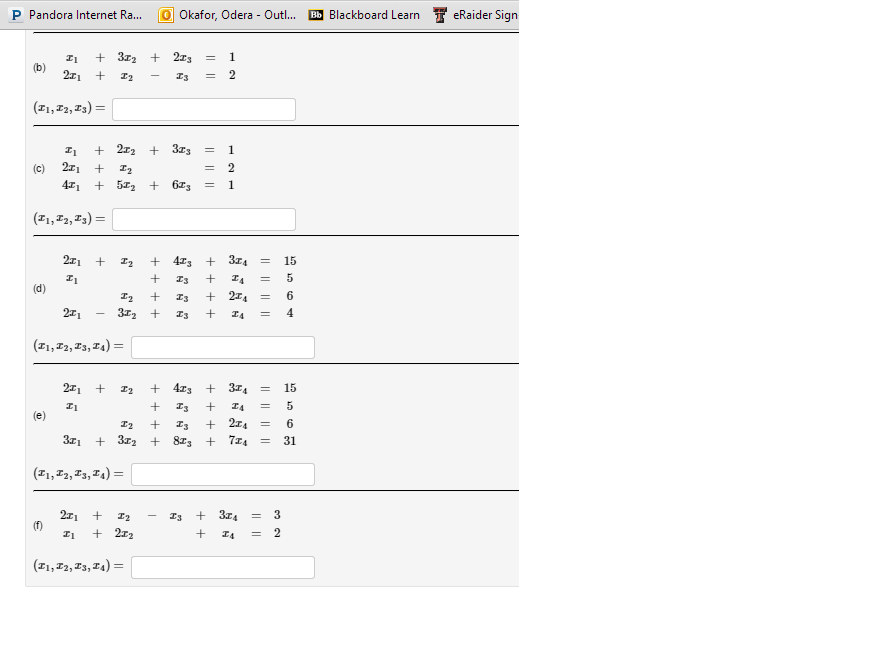
b)………….
AUGMENTED MATRIX =
1	3	2	1
2	1	-1	2
NR2=R2-2R1
1	3	2	1
0	-5	-5	0
-5X2-5X3=0….X2=-X3
X1+3X2+2X3=1…….X1-3X3+2X3=1
X1=1+X3
SOLUTION SET IS ….
X1=	1+X3
X2=	-X3
X3=	X3
WHERE X3 IS ANY REAL NUMBER
C)………….
AUGMENTED MATRIX =
1	2	3	1
2	1	0	2
4	5	6	1
NR2=R2-2R1….NR3=R3-4R1
1	2	3	1
0	-3	-6	0
0	-3	-6	-3
NR1=R1+2R2/3….NR2=R2/(-3)….NR3=R3-R2
1	0	-1	1
0	1	2	0
0	0	0	-3
NO SOLUTION ..
LAST ROW IS CONSISTENT …..0 = 3 ….IMPOSSIBLE
D)………….
AUGMENTED MATRIX =
2	1	4	3	15
1	0	1	1	5
0	1	1	2	6
2	-3	1	1	4
NR1=R1/2….NR2=R2-R1/2….NR4=R4-R1
1	0.5	2	1.5	7.5
0	-0.5	-1	-0.5	-2.5
0	1	1	2	6
0	-4	-3	-2	-11
NR1=R1+R2….NR2=R2/(-0.5)….NR3=R3+2R2….NR4=R4-8R2
1	0	1	1	5
0	1	2	1	5
0	0	-1	1	1
0	0	5	2	9
NR1=R1+R3….NR2=R2+2R3….NR3=-R3…….NR4=R4+5R3
1	0	0	2	6
0	1	0	3	7
0	0	1	-1	-1
0	0	0	7	14
NR1=R1-2R4/7....NR2=R2-3R4/7….NR3=R3+R4/7....NR4=R4/7
1	0	0	0	2
0	1	0	0	1
0	0	1	0	1
0	0	0	1	2
X4=2
X3=1
X2=1
X1=2
IS THE SOLUTION SET……………….ANSWER
E)………….
AUGMENTED MATRIX =
2	1	4	3	15
1	0	1	1	5
0	1	1	2	6
3	3	8	7	31
NR1=R1/2….NR2=R2-R1/2….NR4=R4-3R1/2
1	0.5	2	1.5	7.5
0	-0.5	-1	-0.5	-2.5
0	1	1	2	6
0	1.5	2	2.5	8.5
NR1=R1+R2….NR2=R2/(-0.5)….NR3=R3+2R2….NR4=R4+3R2
1	0	1	1	5
0	1	2	1	5
0	0	-1	1	1
0	0	-1	1	1
NR1=R1+R3….NR2=R2+2R3….NR3=-R3…….NR4=R4-R3
1	0	0	2	6
0	1	0	3	7
0	0	1	-1	-1
0	0	0	0	0
LAST ROW IS ALL ZEROS ..CONSISTENT.
X3-X4=-1………………..X3=X4-1
X2+3X4=7…………..X2=7-3X4
X1+2X4=6…………X1=6-2X4
SO THE SOLUTION SET IS ………………
X1 =	6-2X4
X2=	7-3X4
X3=	X4-1
X4=	X4
WHERE X4 IS ANY REAL NUMBER …ANSWER
b)………….
AUGMENTED MATRIX =
2	1	-1	3	3
1	2	0	1	2
NR1=R1/2…….NR2=R2-R1/2
1	0.5	-0.5	1.5	1.5
0	1.5	0.5	-0.5	0.5
NR1=R1-R2/3……….NR2=R2/1.5…….
1	0	-0.66667	1.666667	1.333333
0	1	0.333333	-0.33333	0.333333
X2+(X3/3)-(X4/3)=1/3………X2=[1/3][1-X3+X4]
X1-(2X3/3)+(5X4/3)=(4/3)
SO THE SOLUTION SET IS ………………
X1 =	[1/3][4+2X3-5X4]
X2=	[1/3][1-X3+X4]
X3=	X3
X4=	X4
WHERE X3 & X4 ARE ANY REAL NUMBERS …ANSWER