MATRICES
------------------
----------------------------------
---------
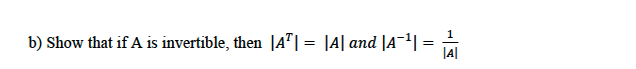
A IS INVERTIBLE ...HENCE A IS NOT SINGULAR ..THAT IS |A| IS NOT EQUAL TO ZERO ..
AS WE KNOW | A | ...DETERMINANT OF ANY SQUARE MATRIX A ...CAN BE FOUND USING CO FACTOR EXPANSION USING ANY PARTICULAR ROW OR COLUMN ..SO IF ....A = [a(I,J)]THEN ...|A|=
, WHERE A(I,K) IS TRHE COFACTOR OF THE ELEMENT a(I,J)....EXPANDING
BY ANY ROW ...
SINCE A TRANSPOSE = [a(J,I)] WE GET .....|A TRANSPOSE | =
...EXPANDING BY ANY COLUMN
SO WE CONCLUDE ..
|A| = | A TRANSPOSE |..............................................PROVED
SINCE DETERMINANT OF PRODUCT OF 2 EQUAL RANKED SQUARE MATRICES = PRODUCT OF DETERMINANTS OF THE 2 WE GET ..
A * A INVERSE = I
|A * A INVERSE| = | I |.........| A | * |A INVERSE | = 1
|A INVERSE | = 1 / | A | | ........PROVED
------------------
For details see post on
26-Feb-2015 at 6:00 am.
----------------------------------
---------
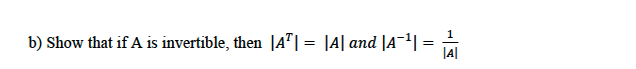
A IS INVERTIBLE ...HENCE A IS NOT SINGULAR ..THAT IS |A| IS NOT EQUAL TO ZERO ..
AS WE KNOW | A | ...DETERMINANT OF ANY SQUARE MATRIX A ...CAN BE FOUND USING CO FACTOR EXPANSION USING ANY PARTICULAR ROW OR COLUMN ..SO IF ....A = [a(I,J)]THEN ...|A|=
SINCE A TRANSPOSE = [a(J,I)] WE GET .....|A TRANSPOSE | =
SO WE CONCLUDE ..
|A| = | A TRANSPOSE |..............................................PROVED
SINCE DETERMINANT OF PRODUCT OF 2 EQUAL RANKED SQUARE MATRICES = PRODUCT OF DETERMINANTS OF THE 2 WE GET ..
A * A INVERSE = I
|A * A INVERSE| = | I |.........| A | * |A INVERSE | = 1
|A INVERSE | = 1 / | A | | ........PROVED
posted by mathsmanagementcommonsense at 4:00 AM
0 Comments:
Post a Comment
<< Home