Hi All ..Really Sorry that I did not up date this for a long long time, though I am pursuing the objectives of this blog at other web sites...
Now that I have a wealth of information thanks to various students who contacted me for help, over the past few years , I now propose to give that through this blog for use of all students in need ...
Here we go ..
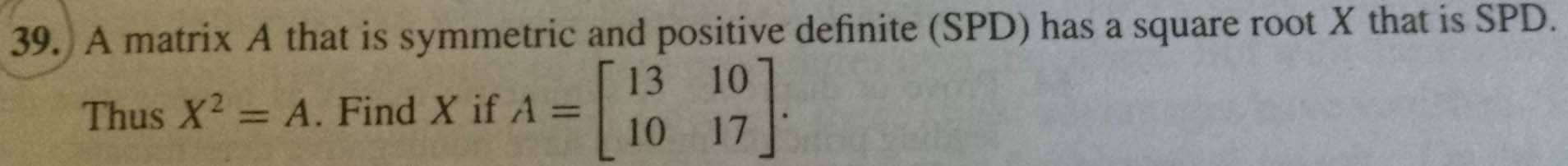
================================================
Now that I have a wealth of information thanks to various students who contacted me for help, over the past few years , I now propose to give that through this blog for use of all students in need ...
Here we go ..
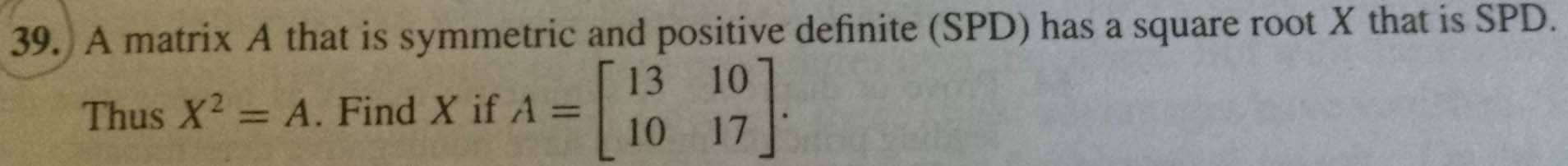
| IN GENERAL WE HAVE …A SYMMETRIC MATRIX A = | ||||||
| A= | ||||||
| B | C | |||||
| C | D | |||||
| IF ITS SQUARE ROOT IS X THEN LET | ||||||
| X= | X^2= | |||||
| P | Q | P^2+QR | PQ+QS | |||
| R | S | RP+SR | RQ+S^2 | |||
| P^2+QR=B……………………1 | ||||||
| Q[S+P]=C………………………2 | ||||||
| R[S+P]=C…………………….3 | ||||||
| S^2+QR=D | ||||||
| EQN. 2 / EQN. 3 , GIVES ...Q = R …………….4 | ||||||
| THIS PROVES THAT X THE SQUARE ROOT OF A | ||||||
| IS A SYMMETRIC MATRIX …………..PROVED ….. | ||||||
| A= | ||||||
| 13 | 10 | |||||
| 10 | 17 | |||||
| X^2=A……LET X BE | X^2= | |||||
| P | Q | P^2+QR | PQ+QS | |||
| R | S | RP+SR | RQ+S^2 | |||
| P^2+QR=13……………………1 | ||||||
| Q[S+P]=10………………………2 | ||||||
| R[S+P]=10…………………….3 | ||||||
| S^2+QR=17 | ||||||
| EQN. 2 / EQN. 3 , GIVES ...Q = R …………….4 | ||||||
| THIS PROVES THAT X THE SQUARE ROOT OF A | ||||||
| IS A SYMMETRIC MATRIX …………..PROVED ….. | ||||||
| EQN. 1 - EQN.2 , GIVES | ||||||
| S^2-P^2=4 | ||||||
| [S+P][S-P]=4………………………………….5 | ||||||
| SOLVING BY XL GOAL SEEK WE GET … | ||||||
| P | Q | R | S | |||
| 0.70642 | 3.535671 | 3.535671 | 2.121092 | |||
| HENCE X = | ||||||
| 0.70642 | 3.535671 | |||||
| 3.535671 | 2.121092 | |||||
| SINCE ALL PRINCIPAL MINORS OF X ARE POSITIVE | ||||||
| X IS POSITIVE DEFINITE | ||||||
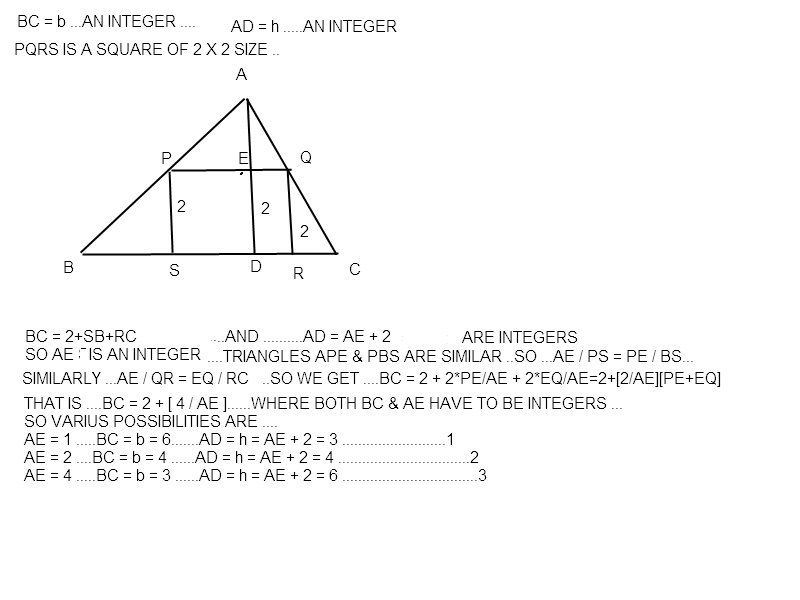
the base b and corresponding height h of a triangle are integers. A 2x2 square is inscribed in the triangle with one side on the given base, and vertices on the other two sides. what are the possible values of the pair (b,h)?



0 Comments:
Post a Comment
<< Home