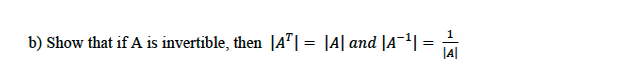-----------------
--------------------------
I =
| 0.5 | x3e?x2dx |
 |
|
| 0 |
----------------
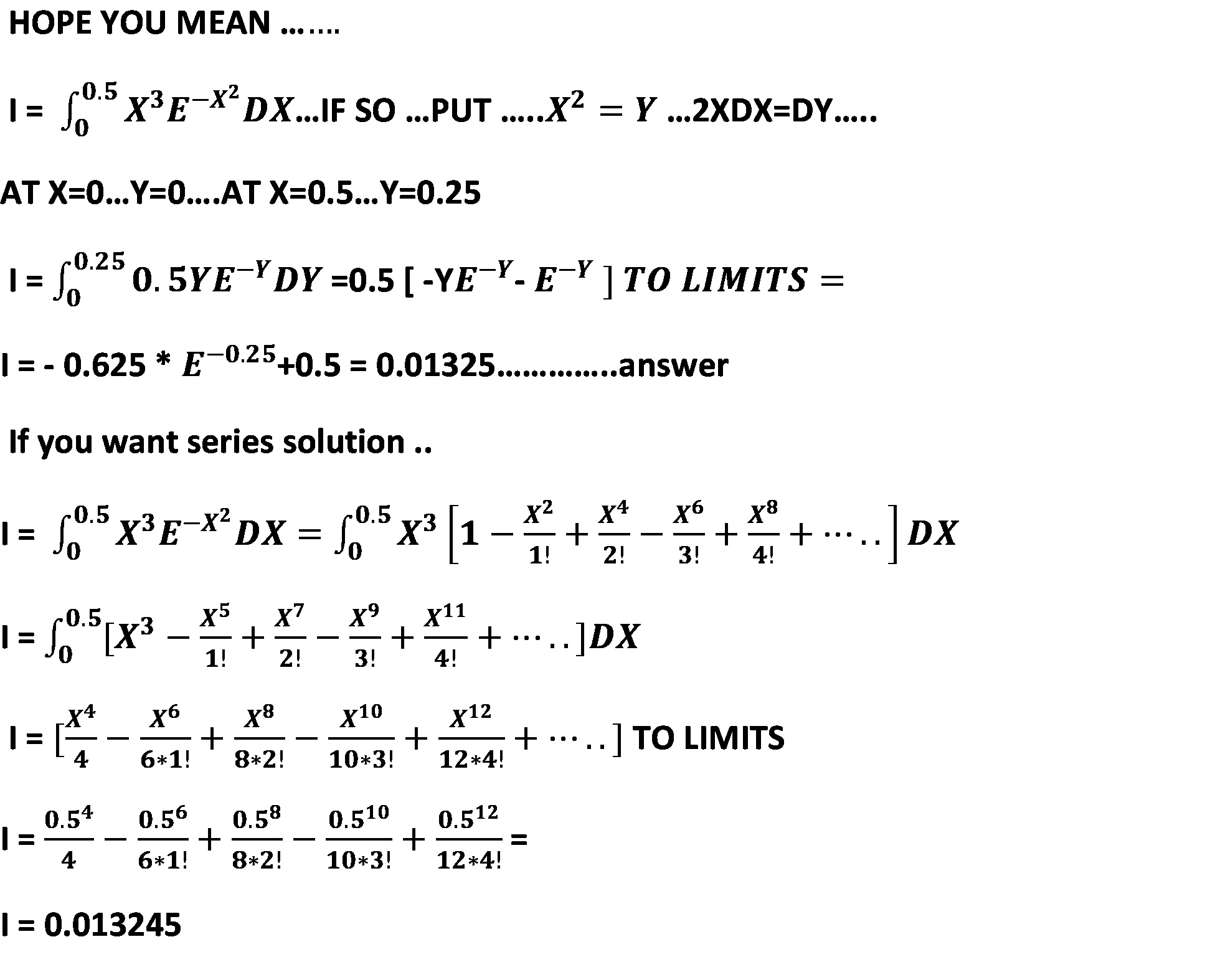
SHARING.... -experiences of teaching maths as a hobby for over 50 years to school and college students. -challenges in project management and the common sense approach to it from old classics.
| 0.5 | x3e?x2dx |
 |
|
| 0 |
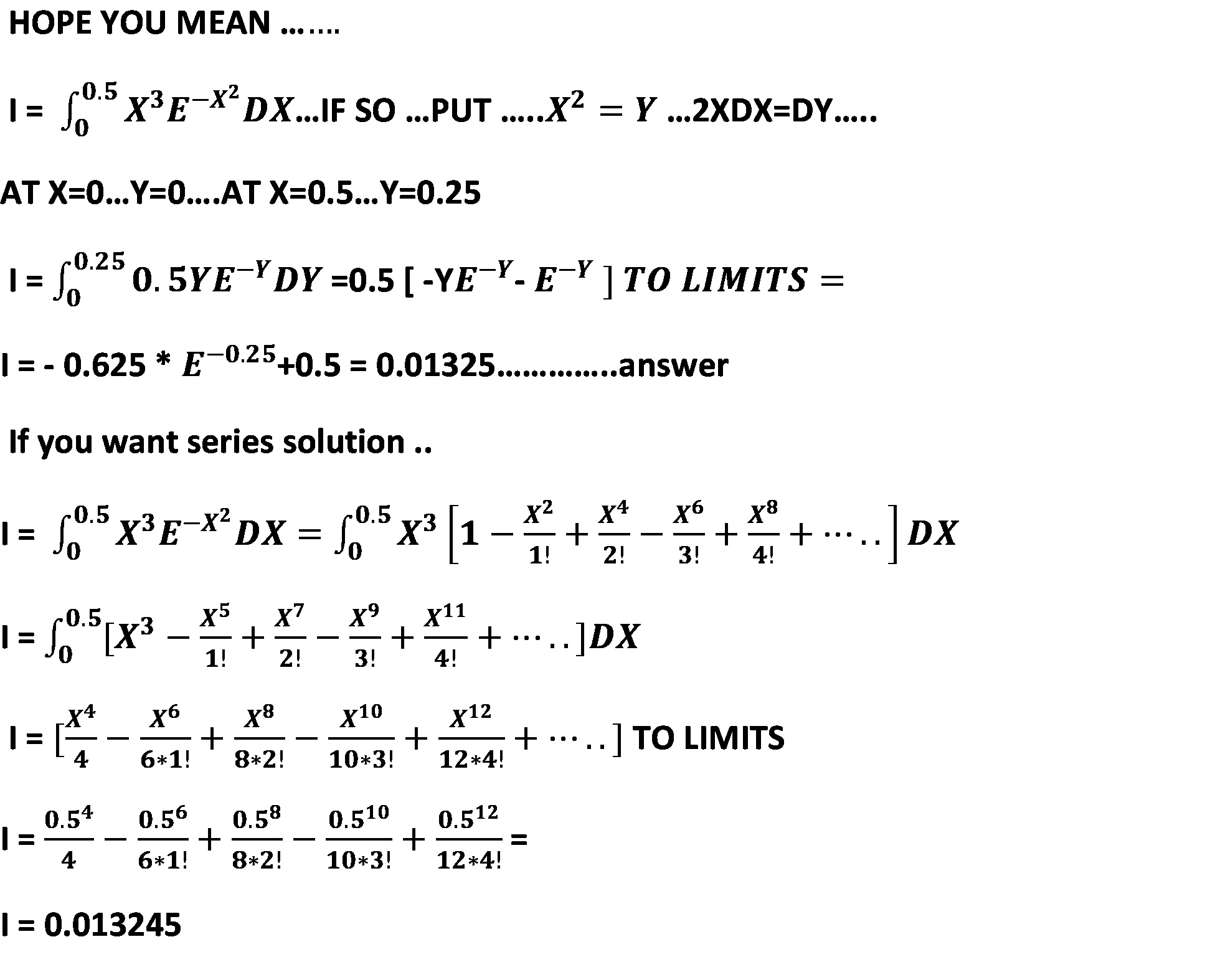


| SURFACE AREA = S = 2[XY+YZ+ZX] = 7000 | |||||||||||
| XY+YZ+ZX=3500……………………………….1 | |||||||||||
| EDGE LENGTH = P= 4[X+Y+Z]=440 | |||||||||||
| X+Y+Z=110……………………………..2 | |||||||||||
| VOLUME=V=XYZ.................................3 |
| FROM EQN. 2 ….X = 110-Y-Z………….4 | ||||||||||
| PUTTING EQN. 1 | ||||||||||
| Z= [3500-XY]/[X+Y]………………..5 | ||||||||||
| PUTTING EQN. 5 IN EQN.4 | ||||||||||
| X=110-Y- | [3500-XY]/[X+Y] | |||||||||
| Y^2+Y[X-110]+[X^2-110X+3500] =0.. | ||||||||||
| Y= | 0.5*[(110-X)+(-3X^2+220X-1900)^0.5] | …OR…. | ||||||||
| Y= | 0.5*[(110-X)-(-3X^2+220X-1900)^0.5] | |||||||||
| WE FIND DISCRIMINANT | D = -3X^2+220X-1900 | - | ||||||||
| D = -[X-10][3X-190 ] ..=0 ..............AT …X = 10 AND ….X= 190/3=63.3333 | ||||||||||
| SO WE GET THE DIMENSIONS &VOLUME AT THE BOUNDARIES AS FOLLOWS | ||||||||||
| NOTE THAT THE FUNCTIONS BEING SYMMETRIC IN X,Y,Z , WE CAN TAKE | ||||||||||
| POINTS AS [10,50,50];[50,50,10];[50,10,50]…AND… | ||||||||||
| [190/3,70/3,70/3] ; [70/3,190/3,70/3] ; [70/3,70/3,190/3] | ||||||||||
| X | Y | Z1 | Z2 | V= | ||||||
| 10 | 50 | 50 | 50 | 25000 | MINIMUM | |||||
| 50 | 50 | 10 | 10 | 25000 | MINIMUM | |||||
| 50 | 10 | 50 | 50 | 25000 | MINIMUM | |||||
| 63.33333 | 23.33333 | 23.33333 | 23.33333 | 34481.481 | MAXIMUM | |||||
| 23.33333 | 63.33333 | 23.33333 | 23.33333 | 34481.481 | MAXIMUM | |||||
| 23.33333 | 23.33333 | 63.33333 | 63.33333 | 34481.481 | MAXIMUM | |||||